Zodiac Wang

通俗理解熵与交叉熵


信息论为我们提供了精确的语言来描述许多事物。对某件事有多么不确信？知道问题A的答案能够为问题B提供多少信息？两组观点之间有多么相似？信息论在不同领域有着非常广泛的应用，从数据压缩，到量子物理，再到机器学习，以及它们的交叉领域。

交叉熵在深度学习领域已然是家喻户晓，但似乎这个概念又不那么好理解。交叉熵的本质到底是什么？这个最早出现在香农毕业论文中的概念，为什么在信息理论中如此重要？

本文是我阅读博文 Visual Information Theory 时的笔记（也可说是我的翻译，因为原文写的非常好，我只在有些地方加上了自己的一点理解），作者用可视化的方法通俗的解释了信息论中的一些基本概念，例如熵和交叉熵。

Table of Contents

可视化概率分布 Visualizing Probability Distributions

将简单的事物可视化，有利于我们理解更复杂的内容。

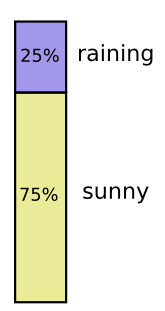
比如说明天有 75% 的概率是晴天，25% 的概率会下雨，那么概率分布可以表示为


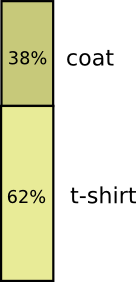
再比如穿衣服，大部分情况下我穿T恤，只有38%的概率穿外套


当这两件事彼此独立、互不相干时，同时可视化这两件事的概率


但如果两件事之间彼此关联，下雨天时我更大可能考虑穿外套，此时概率分布可能是这样


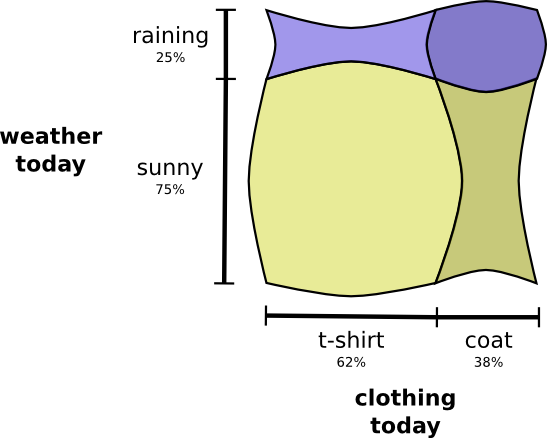
虽然看起来挺有意思，不过这并不能帮助我们理解相关变量的概念。可以先从某一个变量开始考虑，比如天气。其实这就是条件概率conditional probabilities，如果天气晴朗，我有多大可能会穿T恤？如果下雨，我有多大可能穿外套？


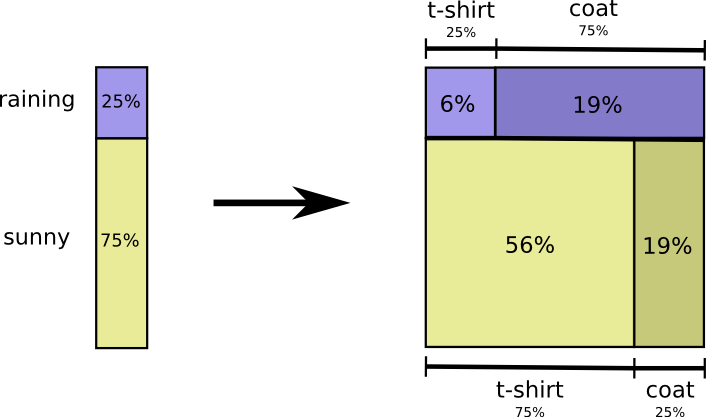
下雨的可能性有25%，如果下雨的话，我有75%的可能穿外套。所以，天下雨并且我穿外套的概率是 75% 乘以 25%，大约是 19%。

下雨并且我穿外套的概率是下雨的概率乘以我在下雨的情况下穿外套的概率。

$$p ( \text { rain, coat } ) = p ( \text { rain } ) \cdot p ( \text { coat } | \text { rain } )$$

这就是概率论中最重要的条件概率公式（贝叶斯定理）：

$$p ( x , y ) = p ( x ) \cdot p ( y | x )$$

通过首先考虑其中某个变量的概率，比如天气，之后再考虑另一个变量的概率，比如穿衣，就得到了在第一个变量确定的情况下另一件事的概率，即条件概率。可以任意选择某一个变量作为第一个变量来考虑，不过还是以天气作为第一个变量吧，这样比较符合直觉。

举个例子，如果随便某一天，我有 38% 的概率穿的是外套，那么假设已经确定我穿的是外套，有多大概率当天是雨天呢？我确实更可能在雨天穿外套而不是晴天，但是实际上雨天的概率在本地是比较小的，实际上当天是雨天的概率为 50%。总结一下，当天下雨并且我穿着外套的概率是，我穿外套的概率（38%）乘以在我穿外套的情况下当天下雨的概率（50%），结果大概为 19%。

$$ p(\text { rain, coat })=p(\text { coat }) \cdot p(\text { rain } | \text { coat }) $$

我们从另一个角度对这两个变量的联合概率进行了可视化，


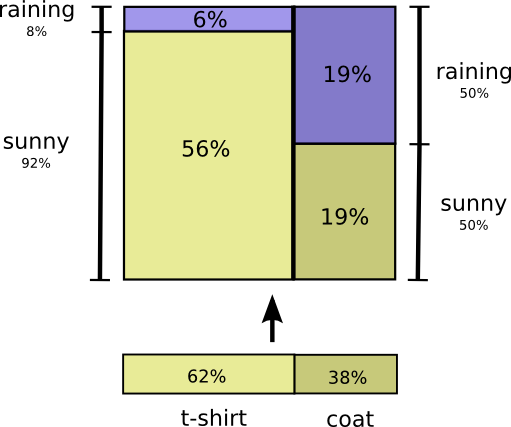
贝叶斯定理实际上就是用来在这两种看问题的不同方式之间相互转换的定理

辛普森悖论 Simpson’s Paradox

辛普森悖论是一个非常反直觉的条件概率例子，研究人员要测试两种肾结石疗法的疗效，一半的病人接受A疗法，另一半接受B疗法。结果表明接受B疗法的病人生存率更高。


但奇怪的是，得小肾结石的病人接受疗法A的生存率更高，而的大肾结石的病人也是接受疗法A生存率更高。一共只有两种肾结石，如果这两种肾结石都是疗法A生存率更高，为什么总体来看，接受疗法B的病人生存率比接受疗法A的病人生存率要高呢？？？

问题的实质在于，最开始研究人员将病人分为两组的时候没有进行充分的随机抽取，导致接受疗法A的病人大部分是患大肾结石的病人，而接受疗法B的病人大部分都是患小肾结石的病人。


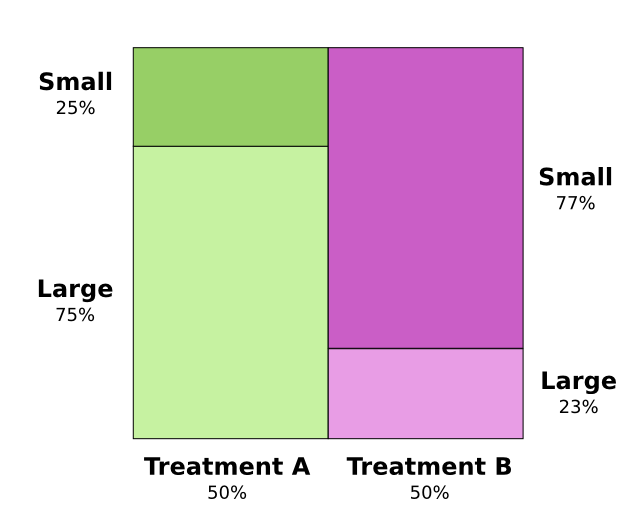
实际上，小肾结石本来就比较容易治愈，无论采用何种疗法。结果导致了这样一个看似悖论的结果。


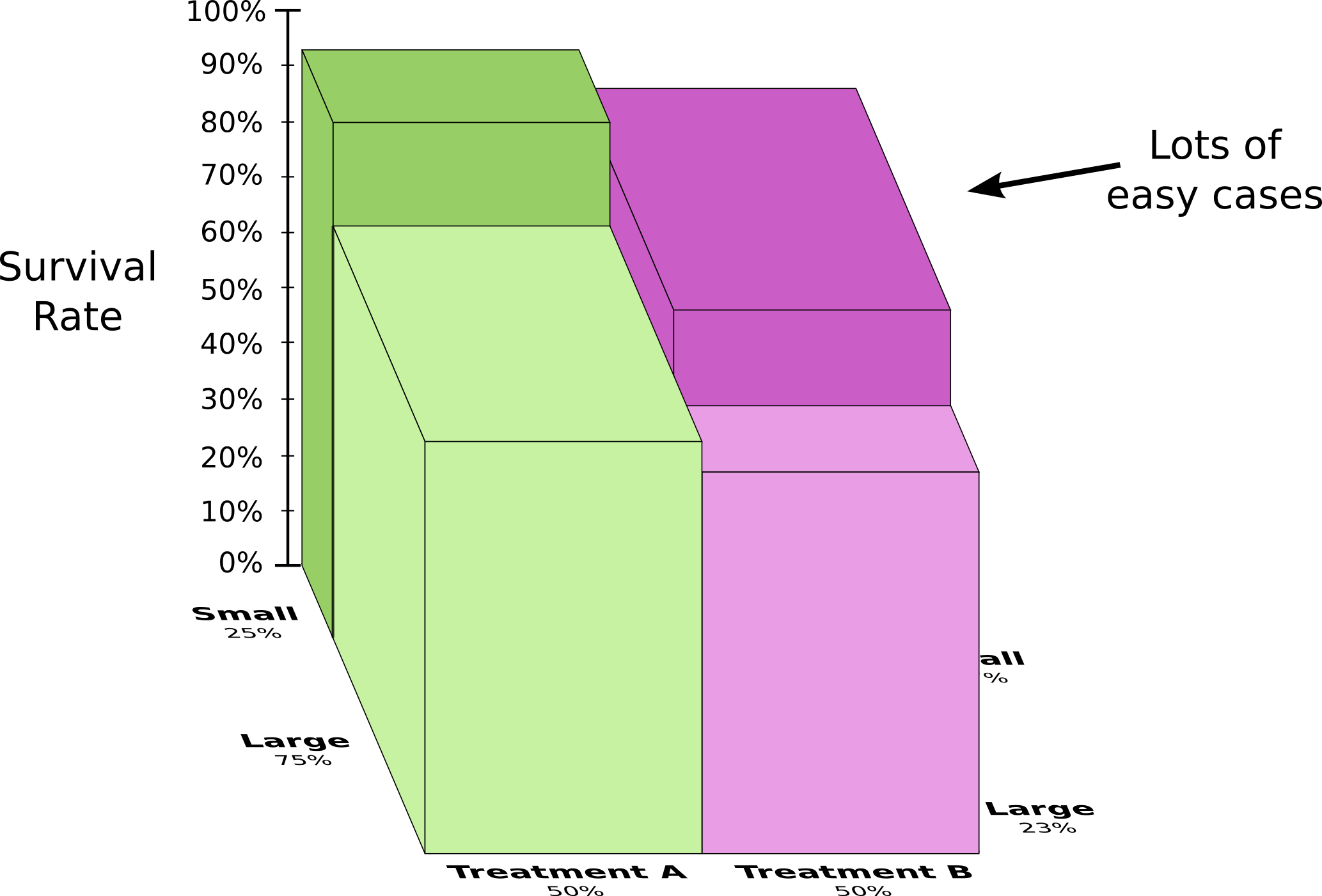
从图上可以看出，无论是大肾结石还是小肾结石，接受A疗法的生存率都比接受B疗法要高。但是将两种结石结合起来看，导致B疗法看起来比A疗法更有效。因为接受B疗法的病人，从一开始就更容易生存（大部分是小肾结石患者）。

编码 Codes

有了基本的概率可视化工具，可以尝试看看信息论里的一些概念。

想象我有一个朋友慧慧，她非常喜欢动物，所以她经常会谈起各种动物。实际上，她只说四个词，“dog”,“cat”,“fish”和“bird”。几个星期之前，慧慧搬到澳大利亚去了，她决定和我只通过发送内容为二进制密码串的短信进行交流。我和她之间发的短信就像这样：


为了理解短信的真实含义，需要对应的密码表，用来对短信中的密码串进行解码。


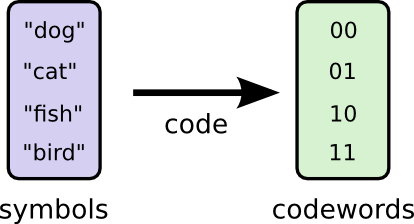
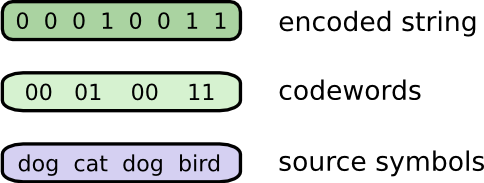
每次需要发交流的时候，我们就把词语替换为相应的密码拼接到一起，形成密码串，然后用短信发送出去。


变长编码 Variable-Length Codes

因为从澳大利亚发短信很贵，每个比特信息要付5美元，慧慧又很能说，必须想办法把短信的平均密码串长度变得更短才行。我注意到慧慧说那些动物词汇的频率各不相同，有些词她经常说，有些词则说的比较少。她很喜欢狗，所以总说”dog“，我们做了个词频表


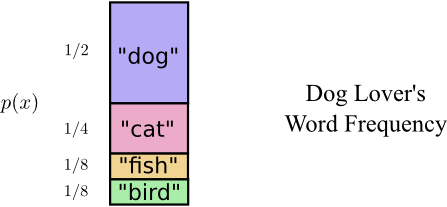
之前的密码表没有考虑每个词的使用频率，所以给每个词的编码长度都是 2 比特，也即是长度为 2.

给编码长度和用词频率做一个可视化，横轴是编码长度，纵轴是用词频率，那么图中所有的彩色面积之和就表示每次发短信时说一个词所需要的密码的期望长度，在这种情况下，显然期望长度为 2 比特。


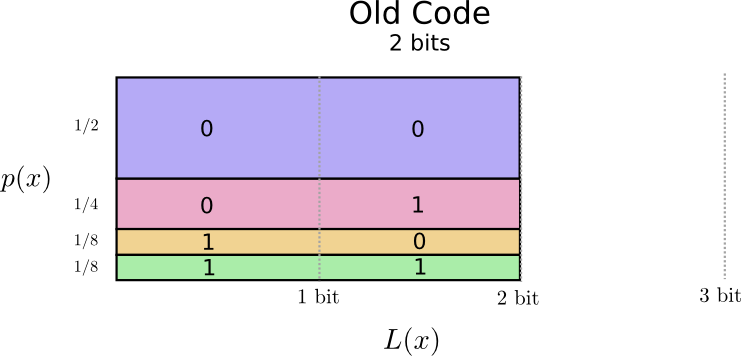
如果可以把所有词的编码都弄的更短就好了，不过这不现实。因为如果某些词的编码缩短了，那么必然有另外一些词的编码长度要增加，否则就会出现混淆（待会解释）。在不能把所有词对应的编码都弄短的情况下，显然，应该把常用的词的编码调短一点。


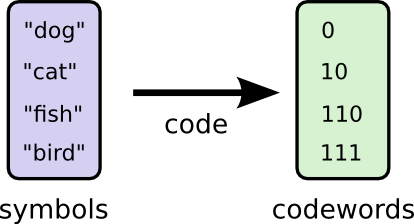
现在每次短信中说一个词的期望密码长度变成了 1.75 比特。


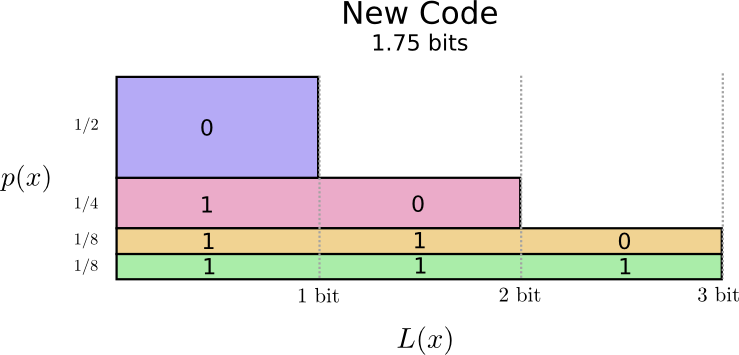
（至于为什么不使用 1 作为 cat 的编码呢？因为这会导致歧义，影响其他所有 1 开头的编码）

实际上，1.75 是这一概率分布（用词频率）下的最优期望密码长度（说一个词）。


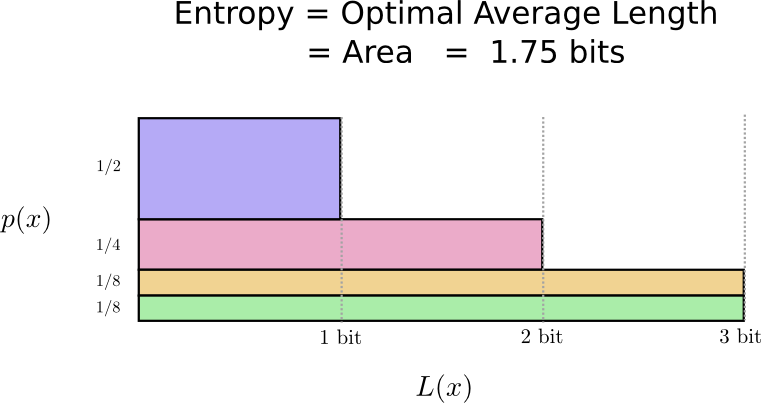
对这一最低限制的理解，最关键是要明白，如果某些词的编码缩短，那么就必然会有别的词的编码会变长。

编码空间 The Space of Codewords

长度为 1 的编码有两个0和1。长度为2的编码有四个，00,01,10和11。每次只要加1比特，编码种数就翻倍。


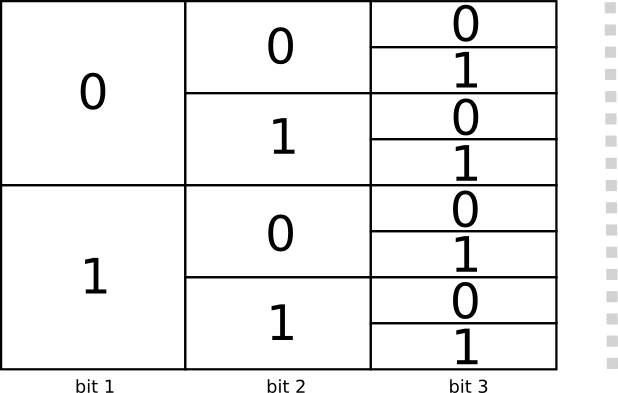
我们关注变长编码，即有些词对应的编码比较长，有些词对应的编码比较短。前文说过，如果每个词都采用相同长度的编码，效果往往并不好。

想想慧慧每次发短信前会怎么做，把每个词对应的密码拼成编码串


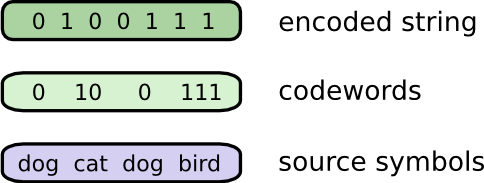
有一个很关键的问题，当我解码的时候，我怎么把这一串编码拆分为对应到每个词的一个个编码呢？如果每个词的编码长度都一样，那还可以每隔几个比特拆分一次，但是现在面临的是边长编码。

另一个可能的解决方案是，有某种固定的编码代表一个词的结尾，但是这种方案太浪费了，我们还是只用 0 和 1。

在这种情况下，很可能出现混淆。比如，0 和 01 分别对应为两个词的编码，那么如果我收到的短信是 0100111 我就不知道第一个 0 到底是 0 还是 01 的开头。为了避免这种情况的发生，必须采取限制，任何编码都不应该是其他编码的前缀（prefix），符合这一规则的编码叫做 prefix codes。

通俗的理解就是，使用较短的编码需要牺牲掉以该编码为前缀的所有可能编码。如果使用编码 01，那么任何以 01 开头的其他编码就都不能用了。比如 010 或者 011010110 等等。


有四分之一的编码是 01 开头的，那么如果取用 01 这一编码，我们就损失了四分之一的编码空间，这就是启用一个 2 比特编码的代价。这是一种权衡，采用更短的编码意味着其他编码更长，那么如何做好这样的权衡呢？

最优编码 Optimal Encodings

作者在此使用了一种直观的证明，我觉得这里作者给出的证明并不那么好理解。下面的证明应该比较简单。

假设对于分布 $X$，每一事件对应编码长度 $l_{i}$，则问题转化为最小化问题

$$ \min _ { l _ { i } } \sum _ { i } p _ { i } l _ { i } $$$$ \text {s.t.} \quad \sum _ { i } r ^ { - l _ { i } } \leq 1 $$

问题可以转化为不等式约束下的拉格朗日数乘法，即

$$ L\left( l_i,\lambda ,u \right) =\sum_i{p}_il_i+\lambda \left( \sum_i{\frac{1}{2^{l_i}}}-1-u^2 \right) $$

求导得，

$$ \left\{ \begin{array}{l} p_i-\lambda \frac{1}{2^{l_{i}}}\ln r=0\\ \sum_i{\frac{1}{2^{l_{i}}}}-1-u^2=0\\ -2\lambda u=0\\ \end{array} \right. $$

显然，$\lambda \neq 0$ 则 $u=0$,故

$$ \frac{1}{2^{l_i}}=\frac{p_i}{\lambda \ln r} $$$$ \sum_i{\frac{1}{2^{l_i}}}=1=\sum_i{\frac{p_i}{\lambda \ln 2}}=\frac{1}{\lambda \ln 2} $$

从而，$\lambda =\frac{1}{\ln 2}$，$l_i=\log _2\frac{1}{p_i}$。

因此按这种基于概率分配编码长度方式得到最优编码分配方式，在发送信息时即对应最短平均编码长度。

计算熵 Calculating Entropy

我们知道，使用长度为 $L$ 的编码，其带来的代价是 $\frac{1}{2^{L}}$ 的编码都不能使用了，反过来已知代价为 cost 则可以求出对应的编码长度 $lenghth = \log _{2}\left(\frac{1}{\operatorname{cost}}\right)$，比如说，对于使用频率为 $p(x)$ 的词 $x$，既然我们按使用频率分配其可支配代价，则其对应的编码长度为 $\log _{2}\left(\frac{1}{p(x)}\right)$，则对应慧慧的词汇使用频率的最优编码长度应为，


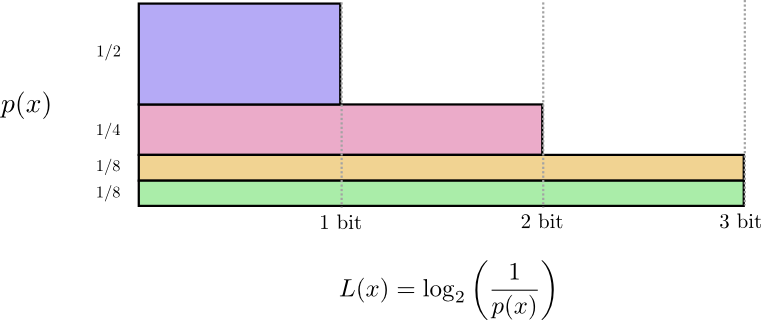
对于服从一定概率分布 $p$ 的事件，若要对其中发生的某件事进行通讯交流，则最短编码长度有一个下界。这一界限，或者说是使用最优编码得到的最优平均编码长度（每个词），就是概率分布 $p$ 的熵 $H(p)$，熵描述了一个概率分布所包含的信息量。

$$ H(p)=\sum_{x} p(x) \log _{2}\left(\frac{1}{p(x)}\right) $$

也记作 $H(p)=-\sum p(x) \log _{2}(p(x))$，前者更符合直觉。

无论怎么修改编码，为了交流这一概率分布下所发生的事件，最优平均编码长度不会低于这一分布的熵。

想象一个场景，慧慧每隔一秒给我发一条短信，短信的内容是一种动物的编码，而她选择每个动物的频率如下，


此时，最优的平均编码长度就是这一概率分布的熵 $H(p)$。

如果我很确定会发生什么事，那么就根本没有发送信息的必要。如果某件事有2种可能，概率分别为 50%，那么我平均只需要发送 1 比特。但是如果有 64 种可能，每种发生的可能性都一样，那么平均需要 6 比特。实际上，如果这些可能性中，每件事发生的概率相对集中，那么所需要的平均编码长度就更短，而如果概率相对分散，那么需要的平均编码长度就更长。

某件事本身越是不确定，当知道发生了什么时，得到的信息也就越多。

熵，即对某个概率分布内所发生的某个事件进行通讯时所需要的最短平均编码长度，或者理解为该分布所包含的信息量

交叉熵 Cross-Entropy

慧慧去澳大利亚前，和涛涛刚刚结婚，涛涛也非常喜欢动物，但是涛涛更喜欢猫，所以他经常说“cat”这个词。


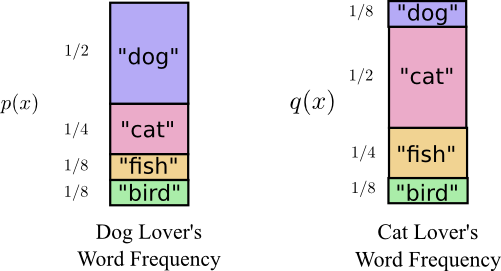
一开始，涛涛给我发信息的时候用的是我帮慧慧制作的密码表，我发现涛涛给我发的信息总是偏长，因为他使用的编码表是我特意针对慧慧的词频分布制作的，慧慧使用自己的密码表给我发送一个词时的平均编码长度是 1.75 比特，而涛涛使用慧慧的编码表给我发送一个动物编码的平均编码长度为 2.25。

使用专门为另一个分布制作的密码表来发送某个分布中事件的信息，此时的平均编码长度定义为交叉熵，

$$ H_{p}(q)=\sum_{x} q(x) \log _{2}\left(\frac{1}{p(x)}\right) $$

(交叉熵有时也写作 $H(p, q)$，但是这一记号与联合熵会发生混淆，而且可能会让人产生交叉熵是具有对称性的误解，实际上分布 $p$ 对分布 $q$ 的交叉熵和分布$q$ 对分布 $p$ 的交叉熵是不一致的。)


所以我帮涛涛也制作密码表，让他使用自己的密码表给我发送信息，结果果然平均编码长度变短了。但是有一次慧慧给我发信息时用了涛涛的编码表，结果她的信息长度变得巨长。

  • 慧慧使用自己的编码表 $H(p)=1.75 bits$
  • 涛涛使用慧慧的编码表 $H_p(q)=2.25 bits$
  • 涛涛使用自己的编码表 $H(q)=1.75 bits$
  • 慧慧使用涛涛的编码表 $H_q(p)=2.375 bits$

特别反直觉，$H_{p}(q) \neq H_{q}(p)$

下面的可视化中，同一列使用相同的编码表，同一行使用相同的词频。


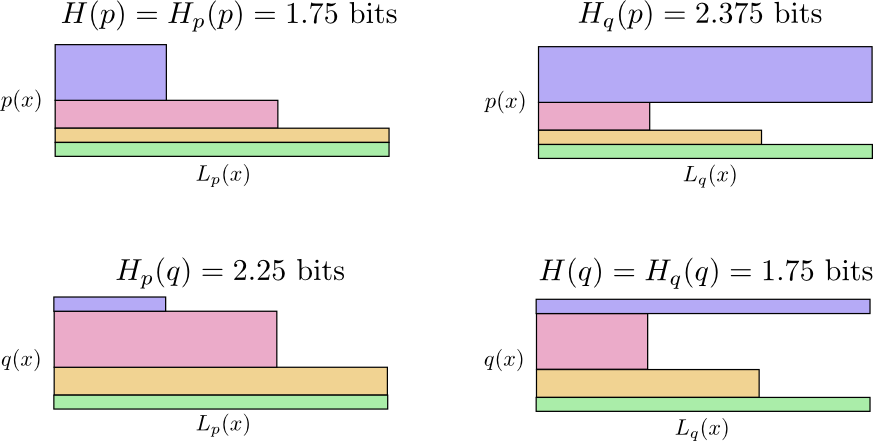
从图中大概可以感受到为什么 $H_{p}(q) \neq H_{q}(p)$。

两个交叉熵的使用场景中，都存在某个词的使用频率很高，同时分配了较长的编码，不过在两个不同的场景中，程度不同，$H_{q}(p)$ 中的蓝色矩形太大了。

交叉熵不具有对称性，但是交叉熵提供了一种描述两个不同的概率分布 $p, q$ 之间差异的方式，分布 $p$ 和分布 $q$ 之间的差异越大，那么 $p$ 对 $q$ 的交叉熵 $H_p(q)$ 与 $p$ 的熵 $H(p)$ 之差就会越大。



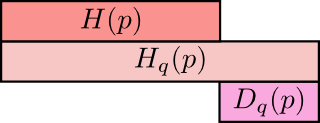
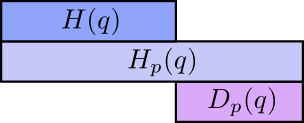
值得注意的是熵与交叉熵之间的差值，这一差值被称为 Kullback–Leibler 散度，或者 K-L 散度，分布 $p$ 对分布 $q$ 的 K-L 散度 $D_q(p)$ 定义为：

$$ D_{q}(p)=H_{q}(p)-H(p) $$

化简K-L散度的表达式，可以得到

$$D_{q}(p)=\sum_{x} p(x) \log _{2}\left(\frac{p(x)}{q(x)}\right)$$

$\log _{2}\left(\frac{p(x)}{q(x)}\right)$实际上是描述编码每个词时两种不同的编码之间的长度差异。

K-L 散度就像是两个分布之间的距离，描述了两个分布之间的差异，在机器学习里 K-L 散度有非常广泛的应用，例如在处理分类问题时，我们希望预测值能够尽可能的接近实际值，这实际上可认为时两个概率分布之间的逼近。之所以说K-L散度像距离，是因为其不具有对诚性，而距离应该是对称的。

交叉熵，即使用针对另一分布制作的密码表对某个分布内的事件进行通讯时的长度，其组成分为两部分：1.使用针对本分布制作的密码表进行通讯时所需的最短平均编码长度；2.因使用针对其他分布的密码表而导致的多出的部分，即KL散度

熵与多变量 Entropy and Multiple Variables

回到天气和穿衣的问题


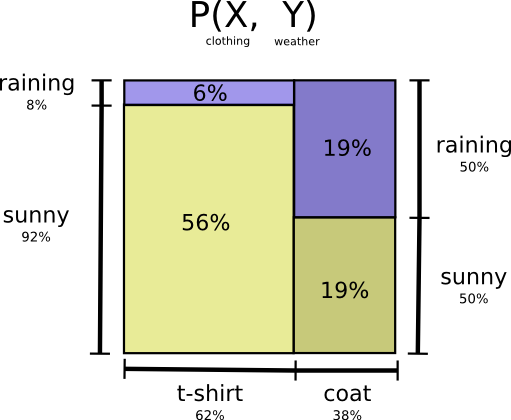
如果我妈关心我有没有穿对衣服，她想知道我这的天气和我穿什么衣服，我得给她发短信，那我需要发几个比特呢？（假设我和妈也通过短信发送编码串进行交流，她也擅长解码），比较简单的思路是将这两件事组合的四种可能转换为一个维度。


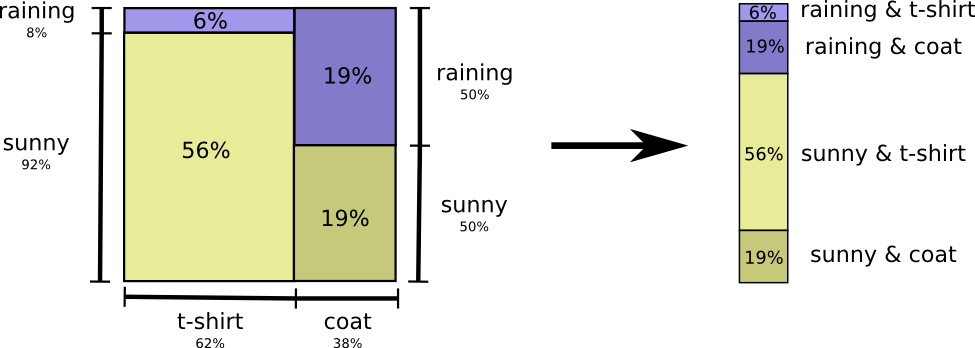
这样就能制定出我的最佳编码表了，同时求出我的平均编码长度


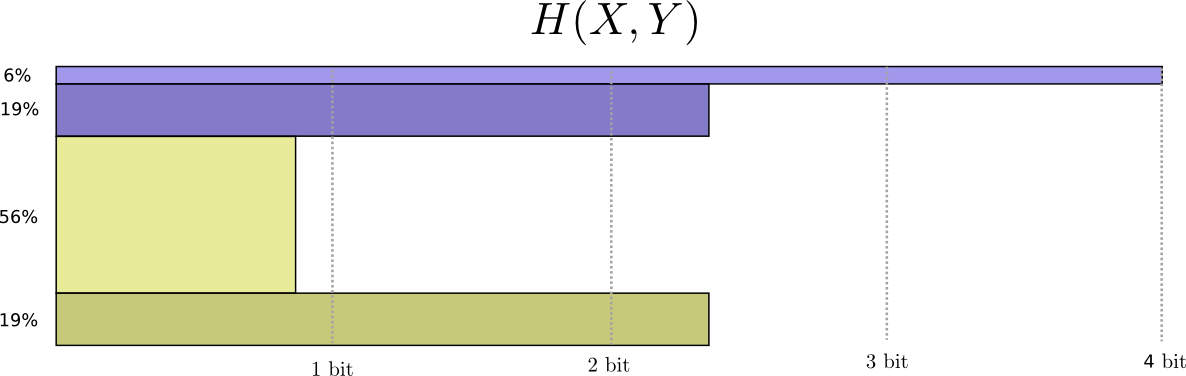
这被称为$X$,$Y$的联合熵

$$ H ( X , Y ) = \sum _ { x , y } p ( x , y ) \log _ { 2 } \left( \frac { 1 } { p ( x , y ) } \right) $$

联合熵，即将两个分布综合起来看得到的对应联合概率分布的熵，与单一分布的熵并无太大区别

这和没有将概率分布一维化之前是完全一样的。

将每种可能的编码长度作为第三个维度可视化，


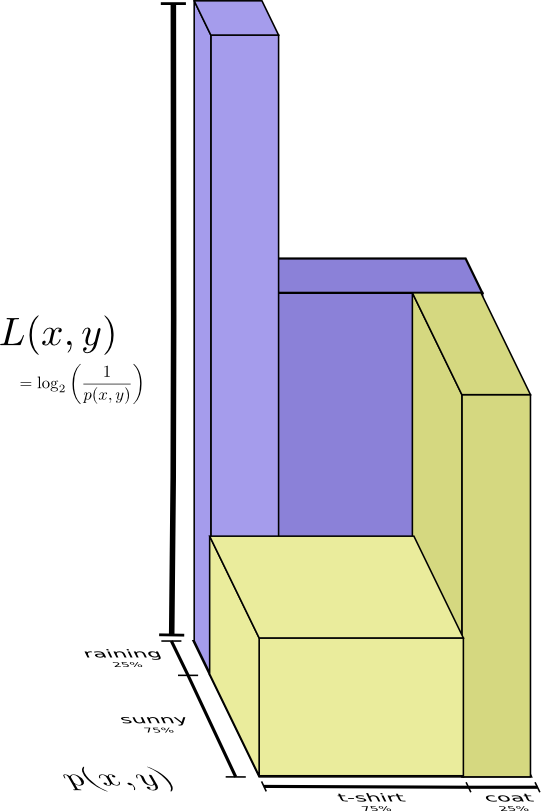
假设我妈已经知道我这的天气了，那我要给她提供多少信息呢？看起来我只要把我穿啥衣服发给她就行了，但其实我并不需要发那么多，她通过今天的天气就已经能推断我大概穿的是什么衣服了。将晴天和雨天分开考虑，如果晴天就是用一套专门为晴天优化的编码表，雨天就用另一套为雨天优化的密码表。这样的话，无论晴天还是雨天，我所需要发送的平均编码长度都比我只使用一套公用的密码表要短。


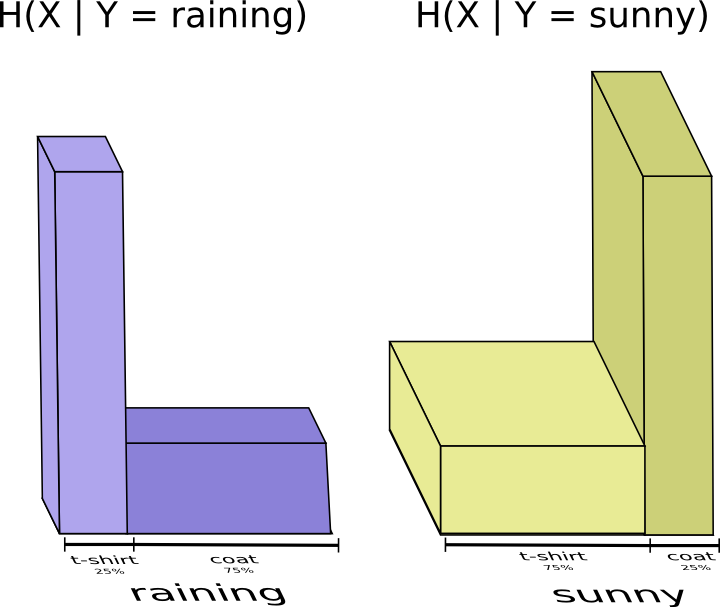
综合来看，只需要把这两种情况结合起来就行,此时只需要 0.81 比特。


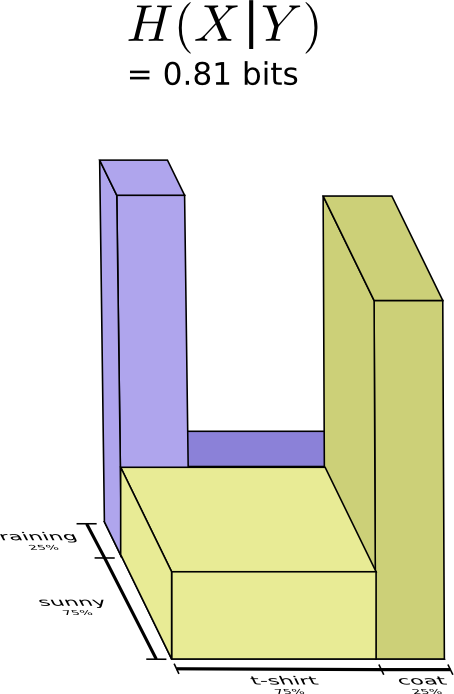
这就是所谓的条件熵

$$ \begin{aligned} H(X | Y) &=\sum_{y} \left(p(y) \sum_{x} p(x | y) \log _{2}\left(\frac{1}{p(x | y)}\right)\right) \\ &=\sum_{x, y} p(x, y) \log _{2}\left(\frac{1}{p(x | y)}\right) \end{aligned} $$

条件熵，在联合概率分布下，已知X后，描述Y所需要的额外信息，比直接描述Y所需的信息（Y的熵）要小。

互信息 Mutual Information

对于两组相关的变量，知道其中的一个意味着我们对另一个也增加了一些认识。即知道其中一个变量的值，在对另一个变量进行通讯的时候，可以少发送一点信息。如果两个变量相关，那么它们的信息应该就有重叠的部分。


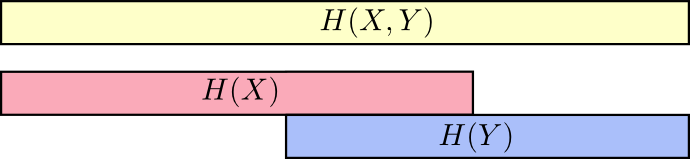
比如说，如果需要同时发送关于 $X$ 和 $Y$ 的信息（联合熵$H(X,Y)$），那么一定比只发送 $X$ 的信息（边缘熵$H(X)$）所需要的平均编码长度要长，但是如果你已经知道了另一个变量 $Y$ 的值，那么此时发送关于 $X$ 的信息（条件熵$H(X | Y)$）所需要的平均编码长度就要比不知道 $Y$ 的时候短一些。


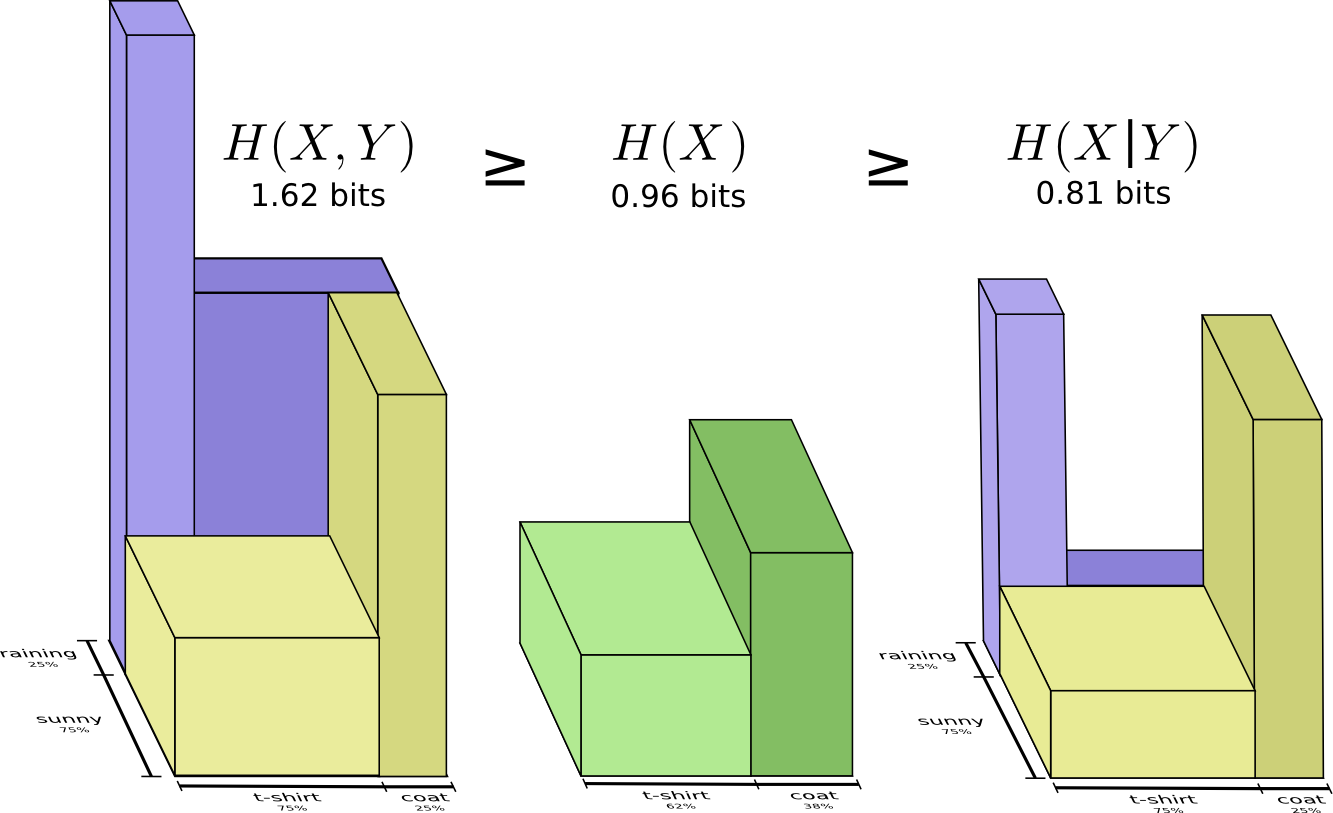
也就是说，$H(X | Y)$是我们和某个已经知道 $Y$ 的值的人交流所需要的最优平均编码长度，但是 $X$ 中的信息并不全部在 $Y$ 中，所以 $H(X | Y)$ 表征的是 $H(X)$ 中不和 $H(Y)$ 重叠的那一部分。


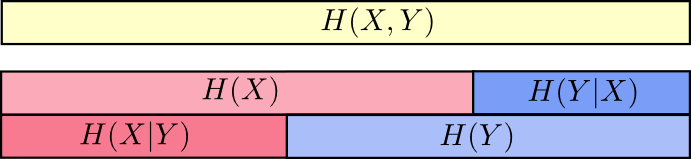
另外一个性质，

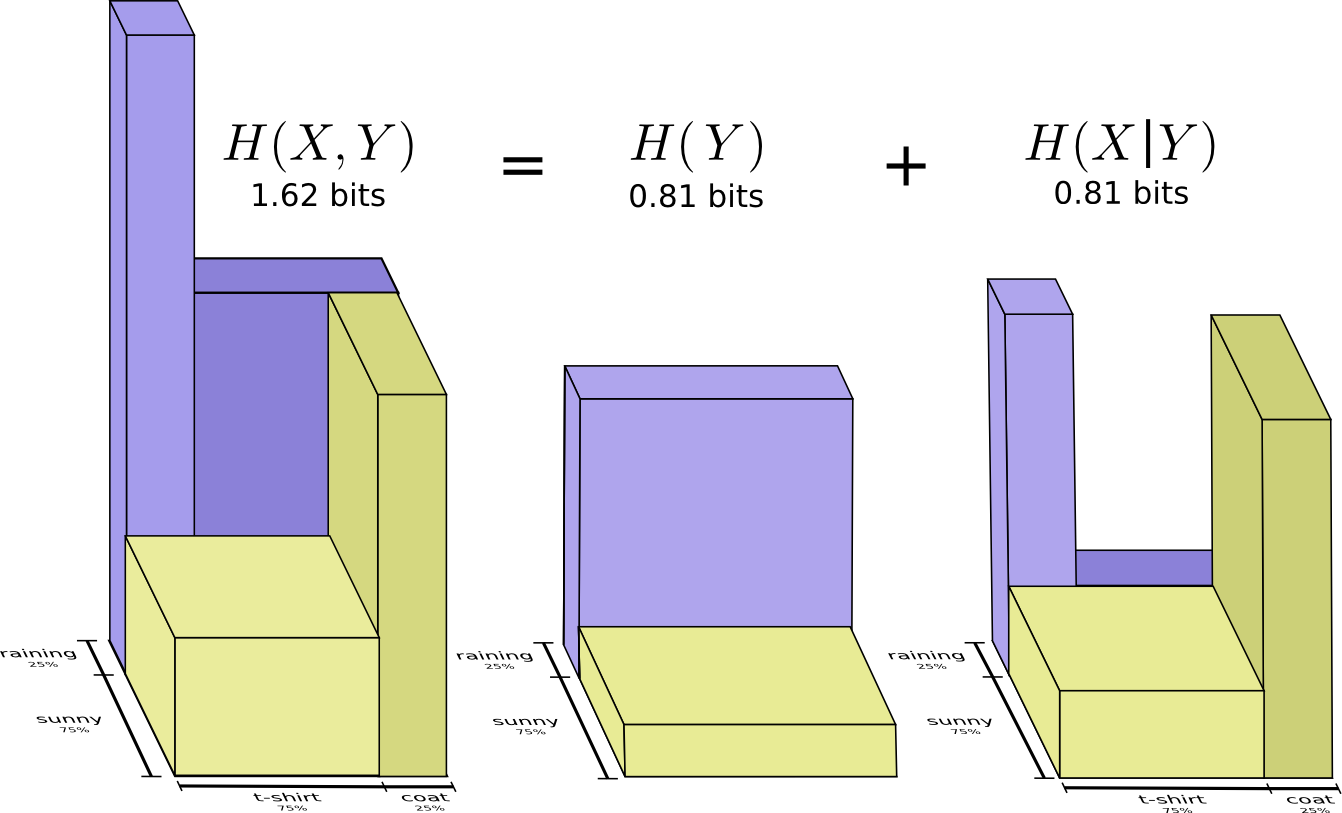
$$H ( X , Y ) = H ( Y ) + H ( X | Y )$$

因为，

$$ \begin{array}{l} H\left( Y \right) \,\,+\,\,H\left( X|Y \right)\\ =\sum_y{\left( p\left( y \right) \log _2\left( \frac{1}{p\left( y \right)} \right) \right)}+\sum_y{\left( p\left( y \right) \sum_x{\left( \left( p\left( x|y \right) \log _2\left( \frac{1}{p\left( x|y \right)} \right) \right) \right)} \right)}\\ =\sum_y{p}\left( y \right) \left( \log _2\left( \frac{1}{p\left( y \right)} \right) +\sum_x{\left( p\left( x|y \right) \log _2\left( \frac{1}{p\left( x|y \right)} \right) \right)} \right)\\ =\sum_y{p}\left( y \right) \left( \sum_x{p}\left( x|y \right) \log _2\left( \frac{1}{p\left( y \right)} \right) +\sum_x{\left( p\left( x|y \right) \log _2\left( \frac{1}{p\left( x|y \right)} \right) \right)} \right)\\ =\sum_y{p}\left( y \right) \left( \sum_x{p}\left( x|y \right) \left( \log _2\left( \frac{1}{p\left( y \right)} \right) +\log _2\left( \frac{1}{p\left( x|y \right)} \right) \right) \right)\\ =\sum_y{p}\left( y \right) \left( \sum_x{p}\left( x|y \right) \log _2\left( \frac{1}{p\left( x,y \right)} \right) \right)\\ =\sum_{x,y}{p}\left( x,y \right) \log _2\left( \frac{1}{p\left( x,y \right)} \right)\\ =H\left( X,Y \right)\\ \end{array} $$

这意味着，描述 X 和 Y 所需的信息（联合熵）是描述 X 自己所需的信息（X的熵）, 加上给定 X 的条件下具体化 Y 所需的额外信息（条件熵）。


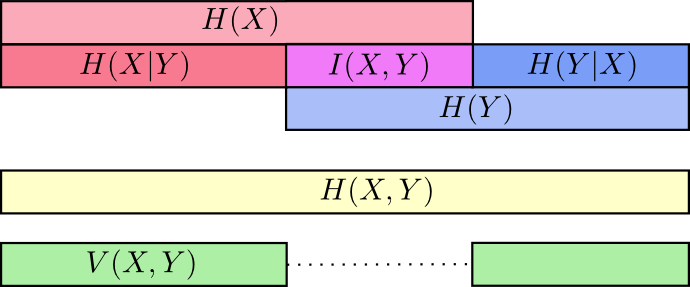
至此，已经从几个方面对 $X$ 和 $Y$ 中的信息进行了理解，有两个分布中的信息 $H(X)$ 和 $H(Y)$，两个分布总体的信息 $H(X, Y)$，其中某个分布独有的信息 $H(X|Y)$ 和 $H(Y|X)$。两个分布之间共有的信息，称为 互信息 $I(X,Y)$

$$I(X,Y) = H(X) + H(Y) - H(X,Y)$$

化简互信息可以得到，

$$ I ( X , Y ) = \sum _ { x , y } p ( x , y ) \log _ { 2 } \left( \frac { p ( x , y ) } { p ( x ) p ( y ) } \right) $$

和 KL 散度很像，因为实际上互信息描述的是，$P(X,Y)$ 和其简单近似 $P(X)P(Y)$ 之间的 KL 散度，用图片来表示的话就是


互信息（Mutual Information，MI）也叫转移信息（transinformation），是两个随机变量间相互依赖的程度，互信息的定义借助了相对熵概念。

和互信息类似，定义变信息 variation of information

$$V(X,Y) = H(X,Y) - I(X,Y)$$

变信息也描述分布之间的差异，和 KL 散度有什么区别呢？ KL 散度描述的是同一组变量，在不同分布上的差异，而变信息描述的是两组（联合分布）变量之间的差异。KL 散度是不同分布之间的差异，变信息描述分布内部的差异。


分数个比特 Fractional Bits

为什么会存在分数个比特呢？上面的例子中，最优编码长度经常是一个分数。可以把这理解为一种平均之后的结果，例如我有一半的概率需要发送1比特，另外一半时间发送2比特，那么平均下来就是1.5比特了，也可以说这是一个概率分布里对应每个事件的最优编码长度的期望平均长度。

但是，为什么单独某个事件对应的编码长度会是分数呢？假设某个概率分布如下，A发生的概率为 71% B 发生的概率为 29%。


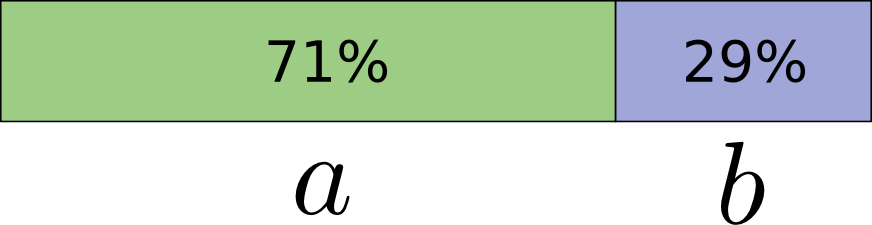
因此，对应A的最佳编码长度为 0.5 比特，B为1.7比特，总体来看最优的平均编码长度是0.848。但如果每次只发送对应一个事件的编码，那么就必然取整数长度的编码，平均来看最优编码长度为1比特（A：1比特；B：1比特）。

如果每次发送的编码串比较长，对应多个事件，如下


此时，理想编码长度如下图，对应最优平均编码长度 1.73


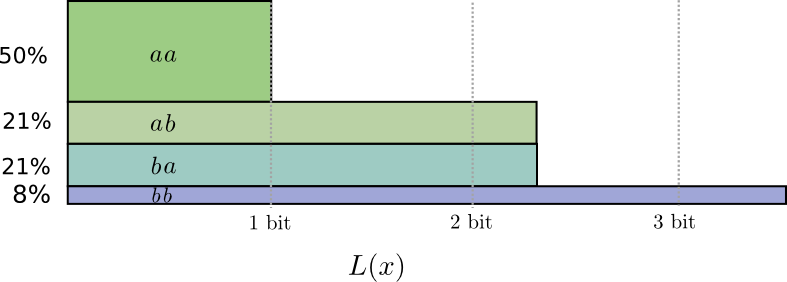
实际的最好编码如下图，对应平均编码长度 1.8，这比分开发送的话对应的 2 比特要少一点。


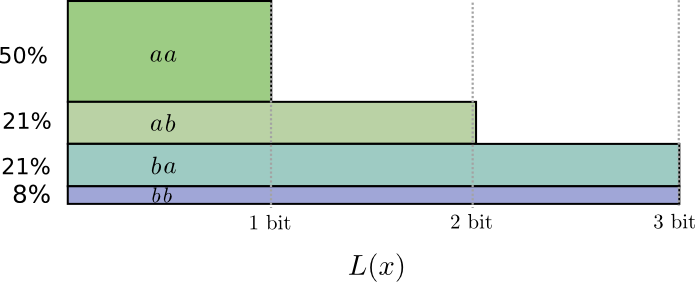
也就是说，平均每个事件 0.9 比特。如果每次发送的编码长度继续变长，每次发送 n 个事件，当 n 趋于无穷，则因为取整而产生的作用将被抵消，最终的编码长度将趋于最优编码长度，也就是 熵（无证明理解）

实际应用中，使用类似Huffman coding或Arithmetic coding这样的编码形式，且只使用二进制编码。

附录

不等式条件约束下的拉格朗日乘数法

拉格朗日乘子法(Lagrange Multiplier)和 KKT(Karush-Kuhn-Tucker)条件是求解约束优化问题的重要方法，在有等式约束时使用拉格朗日乘子法，在有不等约束时使用KKT条件。当然，这两个方法求得的结果只是必要条件，只有当目标函数是凸函数的情况下，才能保证是充分必要条件。

不等式约束下的优化问题通常形式化为：

$$ \begin{array} { c } { \min f ( x, y ) } \\ { \text {s.t.} \quad g ( x, y) \leq 0 } \end{array} $$

比如下列优化问题

$$ \begin{array} { c } { \min f \left( d _ { 1 } , d _ { 2 } \right) = d _ { 1 } ^ { 2 } + d _ { 2 } ^ { 2 } - 2 d _ { 2 } + 2 } \\ { \text {s.t. } \quad d _ { 1 } ^ { 2 } + d _ { 2 } ^ { 2 } \leq 4 } \end{array} $$

$\lambda$ 是拉格朗日乘子，引入的新的 $\eta^2$ 是一个松弛变量，目的是为了将不等式约束经过松弛后，变为等式约束，注$\lambda≥0$。这是不等式约束与等式约束最优化问题拉格朗日乘数法的一个重要区别。转化为等式约束优化问题。

$$ g \left( d _ { 1 } , d _ { 2 } , \lambda , \eta \right) = f \left( d _ { 1 } , d _ { 2 } \right) + \lambda \left( d _ { 1 } ^ { 2 } + d _ { 2 } ^ { 2 } - 4 + \eta ^ { 2 } \right) $$

对所有变量求导

$$ \left\{ \begin{array} { l } { 2 d _ { 1 } + 2 \lambda d _ { 1 } = 0 }\\ { 2 d _ { 2 } - 2 + 2 \lambda d _ { 2 } = 0 }\\ { d _ { 1 } ^ { 2 } + d _ { 2 } ^ { 2 } - 4 + \eta ^ { 2 } = 0 }\\ { 2 \eta \lambda = 0 } \\ { \lambda \geq 0 } \end{array} \right. $$

由$2 \eta \lambda = 0$, 知 $\eta=0$或$\lambda=0$，由$ 2 d _ { 1 } + 2 \lambda d _ { 1 } = 0$ 知 $d_{1}=0$或$\lambda=-1$。

若 $\lambda=0$，则 $\lambda\ne-1$ 则 $d_{1}=0$,故有 $d _ { 2 } = 1 , \eta = \sqrt { 3 }$

若 $\eta=0$，已知 $\lambda \geq 0$,则 $d_{1}=0$，故有$d _ { 2 } = 2, \lambda= -\frac{1}{2} $

机器学习里的交叉熵

  • Softmax和交叉熵的深度解析和Python实现 SoftMax 损失函数推导
  • Neural Network and Deeplearning-CrossEntropy

    书中描述了另外一种应用交叉熵的形式，即不使用 SoftMax 而在最后一层直接使用交叉熵，但此时的交叉熵表述形式与常用的表现形式 $$L = -\sum_{i}y_{i}log(p_{i})$$ 略有不同,表现形式为 $$L = -\sum_{i}(y_{i}log(p_{i})+(1-y_{i})log(1-p_{i}))$$ 最终结果都是 $$\frac{\partial L}{\partial z_{i}}=p_{i}-y_{i}$$ 值得注意的是，这两种形式不可更换，否则结果将不具有上式的简单形式

两种交叉熵形式不同的原因主要是因为其前一层的输出分布不同，经过SoftMax处理后的分数，整体上可以视为一个分布，所以可以直接使用交叉熵公式，而使用Sigmoid产生的输出，其和并不为1所以不能视为一个分布，故只能将每个神经元视为一个二元分布

如何理解 KL 散度的非对称性

选择哪一种KL散度取决于实际问题，各有特点

机器学习分类问题中使用的是正向KL散度，即以原始数据分布作为权值（事件发生概率），估计分布作为编码方式，通过反向传播优化交叉熵。

总的来说，正向Kl散度偏向全面覆盖，反向KL散度可能锁定原始分布的某一个峰值。


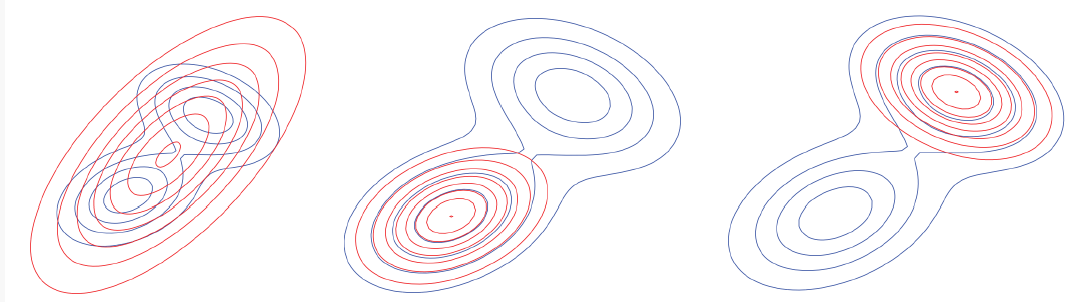
左边红色分布为基于正向KL散度对真实分布进行的估计，中间和右边为反向KL散度。

JS 散度（Jensen-Shannon divergence）

将正反KL散度结合，JS散度具有对称性，真正可以称得上是距离度量。

机器学习中交叉熵与 KL 散度的等价性

机器学习中目标数据的分布式确定的，因此交叉熵与KL散度之间仅相差一个常数（真实数据分布的熵）。因此最小化交叉熵和最小化KL散度等价，而交叉熵更好计算所以就使用交叉熵。

交叉熵损失、对数损失和最大似然估计的等价性

作者提供了一个不错的思路，解释了 softmax 回归和 logistic 回归之间的统一联系，softmax 回归对应多分类问题，logistic回归对应二分类问题，logistic 是 softmax 的一种退化。

那么思考一下，使用sigmoid 激活函数进行学习的多分类问题是怎样一种情况？softmax 回归是整个输出层神经元的输出整体可看做一个概率分布（和为1），而使用 sigmoid 函数激活的神经网络最后一层，只能把每个神经元被看作一个二分类任务。

其他参考资料

Published

Category

posts

Tags

Contact